Advanced API¶
strainpycon.integration¶
Functions related to posterior density integration.
-
strainpycon.integration.mean_var(mat_blocks, d, gamma, quad_nodes)¶ Computes the posterior mean and variance for the strain components.
This function is not meant to be called directly. See posterior_stats method in StrainRecon class for a more convenient function.
Parameters: - mat_blocks (2D- or 3D-array) – All possible binary rows (2D) or blocks (3D) in the matrix.
- d (vector) – The measurement vector in StrainRecon.jl format.
- gamma (vector) – Standard deviation of the assumed Gaussian measurement noise. Same shape as d.
- quad_nodes (2D array) – Each row is a quadrature node. Nodes have equal weights.
Returns: - meanmat (2D array) – Posterior mean of the matrix. Full matrix is returned instead of StrainRecon.jl format, if mat_blocks is 3D.
- meanvec (vector) – Posterior mean of the vector.
- varmat (2D array) – Diagonal elements of the posterior covariance of the matrix. Full matrix is returned if mat_blocks is 3D.
- varvec (vector) – Diagonal elements of the posterior covariance of the vector.
Notes
See [1] for the algorithm.
References
[1] “A Bayesian framework for molecular strain identification from mixed diagnostic samples”, L. Mustonen et al, https://doi.org/10.1088/1361-6420/aad7cd
strainpycon.psimplex¶
Numerics for the probability simplex.
Probability simplex contains  -dimensional vectors
-dimensional vectors 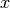 that
satisfy
that
satisfy 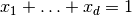 and
and  for
for
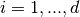 .
.
-
strainpycon.psimplex.lstsq_bilin(mat_rows, b, weights=None, trials=100, target_norm=0.0, vecstep=1e-08, veciters=100)¶ Least-squares solution to a constrained bilinear system.
Finds a matrix
 in some finite set and a vector
in some finite set and a vector 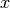 in the
probability simplex such that the sum of squares
in the
probability simplex such that the sum of squares 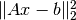 is minimized. More generally, finds a minimizing matrix and vector for the
weighted sum
is minimized. More generally, finds a minimizing matrix and vector for the
weighted sum  , where the
weights
, where the
weights  are given.
are given.The rows in the matrix are restricted to the set provided by the user. Alternatively, instead of rows, the user may also provide the feasible blocks that can be stacked vertically to form the minimizing matrix.
Parameters: - mat_rows (array) – If the shape is (K, N), then each row in the output matrix a is a row in mat_rows. If the shape is (K, P, N), then a contains blocks of shape (P, N), stacked on top of each other, such that each block is mat_rows[i] for some i. In both cases, repetitions are allowed in a.
- b (vector) – “Right hand side” vector. If the shape of mat_rows is (K, P, N), then the length of b must be divisible by P.
- weights (None or array, optional) – If None (default), unweighted least-squares problem is considered. Otherwise must have as many elements as there are blocks in a (i.e., the length of b divided by P).
- trials (int, optional) – Number of initializations for the BCD method. Higher value requires more time, but makes finding global minimizers more likely. Default is 100.
Returns: - a (array) – Minimizing matrix with shape (M,N), where M is the length of b.
- x (vector) – Minimizing vector with shape (N,).
- trials (int) – Actual number of BCD trials.
- resnorm (float) – Residual (non-squared) norm || ax - b ||, or weighted norm if weights is an array.
Other Parameters: - target_norm (float, optional) – Do not start new instances of the BCD method if the (weighted) residual norm goes below this value. Default is 0 which means that BCD is initialized trials times unless exact minimizers are found (which is usually very unlikely).
- vecstep (float, optional) – Step size stopping criterion in the simplex-constrained least squares problem, passed as minstep to strainpycon.psimplex.lstsq_simplex.
- veciters (int, optional) – Maximum number of iterations in the simplex-constrained least squares problem, passed as maxiter to strainpycon.psimplex.lstsq_simplex.
See also
Notes
This function employs the block coordinate descent (BCD) method which alternately minimizes the matrix (for a fixed vector) and the vector (for a fixed matrix). The initial vectors are drawn uniformly from the probability simplex.
For each output (a, x) there exist factorial of N equally good solutions corresponding to different ordering of the rows in a and the elements in x. Due to implementation details, the output is “biased” towards some orderings. More precisely, x is often sorted in descending order.
Examples
Restrict a to be a binary matrix with three columns. Therefore, x has also three elements.
>>> import numpy as np >>> import strainpycon >>> import itertools >>> mat_rows = np.array(list(itertools.product([0,1], repeat=3))) >>> mat_rows array([[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 1, 1], [1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]]) >>> b = np.array([0, 0.97, .49, .51]) >>> result = strainpycon.lstsq_bilin(mat_rows, b) >>> result[0] array([[0, 0, 0], [1, 1, 0], [0, 1, 0], [1, 0, 1]]) >>> result[1] array([0.48, 0.49, 0.03]) >>> # The solution is an exact match: >>> np.dot(result[0], result[1]) array([0. , 0.97, 0.49, 0.51])
Let us now assume that an even row in a must always be the “negation” of the previous row.
>>> mat_rows2 = np.array([mat_rows, 1-mat_rows]).swapaxes(0,1) >>> mat_rows2.shape (8, 2, 3) >>> mat_rows2 array([[[0, 0, 0], [1, 1, 1]], [[0, 0, 1], [1, 1, 0]], [[0, 1, 0], [1, 0, 1]], [[0, 1, 1], [1, 0, 0]], [[1, 0, 0], [0, 1, 1]], [[1, 0, 1], [0, 1, 0]], [[1, 1, 0], [0, 0, 1]], [[1, 1, 1], [0, 0, 0]]]) >>> result2 = strainpycon.lstsq_bilin(mat_rows2, b) >>> result2[0] array([[0, 0, 1], [1, 1, 0], [0, 1, 1], [1, 0, 0]]) >>> result2[1] array([0.51, 0.475, 0.015]) >>> # This time the residual does not go to zero: >>> np.dot(result[0], result[1]) array([0.015 , 0.985, 0.49, 0.51])
Notice that because the method uses random numbers, the results may be different than shown above.
-
strainpycon.psimplex.lstsq_simplex(a, b, minstep=1e-08, maxiter=100)¶ Least-squares solution to a simplex-constrained linear equation.
Finds a vector
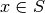 that minimizes
that minimizes 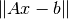 with
with
 denoting the probability simplex.
denoting the probability simplex.Parameters: - a (array) – Any real matrix
 . (should be tall?)
. (should be tall?) - b (vector) – “Right hand side” vector.
- minstep (float, optional) – Stopping criterion parameter. The APG iteration stops when the norm between subsequent iterates goes below this value.
- maxiter (int, optional) – Maximum number of iterations. Set to zero to use minstep as the only stopping criterion.
Returns: - sol (vector) – Minimizing vector.
- iters (int) – Number of APG iterations (0 means no APG was needed).
Notes
This function first tries to solve the problem without non-negativity constraints by using a KKT-like matrix for the sum-to-one equality constraint. If the resulting vector contains negative values, then the iterative accelerated projected gradient (APG) method [2] is employed.
The APG method is fast if the condition number of the matrix is small. In particular, if the matrix is rank-deficient, then APG may need a lot of iterations to converge. In the latter case, the minimizing vector may also be non-unique. One of the minimizing vectors is then returned.
References
[2] “Least-squares on the simplex for multispectral unmixing”, L. Condat, http://www.gipsa-lab.grenoble-inp.fr/~laurent.condat/publis/Condat-unmixing.pdf - a (array) – Any real matrix
-
strainpycon.psimplex.ordered_mean(dim, order=1)¶ Centroid of the sorted vectors of the probability simplex.
The centroid means the expected vector when vectors are drawn uniformly from that part of the simplex that satisfies the ordering constraint.
Parameters: - dim (int) – Number of elements in the vector.
- order ({1, -1}, optional) – If 1 (default), the elements are sorted in ascending order. If -1, the elements are in descending order.
Returns: mean_vec – Centroid, or expected vector.
Return type: vector with shape (dim,)
Notes
See [3] for the algorithm.
References
[3] https://mathoverflow.net/a/238524
-
strainpycon.psimplex.proj_simplex(vec)¶ Euclidean projection of a given vector onto the probability simplex.
Parameters: vec (vector) – Vector to be projected. Shape can be (dim,), (dim, 1), or (1, dim). Returns: Same shape as the input. Return type: vector Notes
This function uses an exact, non-iterative algorithm from [4].
References
[4] “Projection onto the probability simplex: An efficient algorithm with a simple proof, and an application”, W. Wang and M. Á. Carreira-Perpiñán, https://arxiv.org/abs/1309.1541
-
strainpycon.psimplex.rand_simplex(dim, count=None, sort=0)¶ Draw uniform random vectors from the probability simplex.
Parameters: - dim (int) – Number of elements in a vector.
- count (None or int, optional) – Number of vectors. The default is None which corresponds to a single vector.
- sort ({0, 1, -1}, optional) – When sort equals 0 (default), the vectors are not sorted. If sort is 1, each vector is sorted in ascending order, and if sort is -1, each vector is sorted in descending order.
Returns: If count is None, the shape of the output is (dim,). Otherwise, the shape is (count, dim).
Return type: ndarray
Notes
Sorting the vectors after uniformly drawing them from the probability simplex is equivalent to drawing them uniformly from the specific part of the simplex that contains the ordered vectors.
This function relies internally on numpy.random.random_sample when drawing random numbers.
strainpycon.utils¶
Simple auxiliary functions performing conversions etc.
-
strainpycon.utils.addnanrows(mat, nanlocs)¶ Returns array with nan rows added to specific locations.
Parameters: - mat (2D- or 3D-array) – If mat is 3D, then the rows are added to mat[i] for each i.
- nanlocs (bool vector) – Vector specifying the nan row indices in the returned matrix. True corresponds to nan. The shape must be (k,), where k equals (number of rows in mat) + (number of Trues in nanlocs).
Returns: mat – Array augmented with nans.
Return type: 2D- or 3D-array
-
strainpycon.utils.binary_blocks(n, cats=2)¶ All possible binary rows or blocks.
Returns either all possible binary vectors having given number of elements, or all possible binary blocks having given number of columns and column sums of at most one.
Parameters: - n (int) – Number of elements in a vector or number of columns in a block.
- cats (int, optional) – Number of categories for each column in a block. Must be at least 2. If cats is 2 (default), then a column can be either 0 and 1, i.e., a scalar. Otherwise, there are cats-1 different columns having sum of at most one.
Returns: blocks – If cats is 2, the shape is (2**n, n). Otherwise, the shape is (cats**n, cats-1, n).
Return type: 2D- or 3D-array
Examples
>>> from strainpycon.utils import binary_blocks >>> binary_blocks(2) array([[0, 0], [0, 1], [1, 0], [1, 1]]) >>> binary_blocks(2, cats=3) array([[[0, 0], [0, 0]], [[0, 1], [0, 0]], [[0, 0], [0, 1]], [[1, 0], [0, 0]], [[1, 1], [0, 0]], [[1, 0], [0, 1]], [[0, 0], [1, 0]], [[0, 1], [1, 0]], [[0, 0], [1, 1]]])
-
strainpycon.utils.binmat2intmat(binmat, cats)¶ Converts binary block matrix to a non-negative integer matrix.
This function is the inverse of pystrainrecon.utils.intmat2binmat function.
Parameters: - binmat (2D array) – Binary block matrix where blocks have cats-1 rows and each column in a block sums up to 1 or 0.
- cats (int) – Size of the block plus one. Must be at least 2.
Returns: intmat – Matrix with integers {0, …, cats-1}.
Return type: 2D array
See also
Example
>>> mat = np.array([[0, 1, 0], [0, 0, 1], [0, 1, 0], [1, 0, 0]]) >>> mat array([[0, 1, 0], [0, 0, 1], [0, 1, 0], [1, 0, 0]]) >>> binmat2intmat(mat, 3) array([[0, 1, 2], [2, 1, 0]])
-
strainpycon.utils.handle_input(meas, gamma)¶ Converts the user input for computational measurements and noise levels.
Typically, the user should not call this function directly.
-
strainpycon.utils.intmat2binmat(intmat, maxint)¶ Converts non-negative integer matrix to a binary matrix.
Every positive integer k is converted to a unit vector which has one in the k’th position (when counting starts from one) and zero in the remaining positions. Zero is converted to a zero vector. The returned matrix has the same number of columns as the input matrix, i.e., the conversion is performed vertically.
Parameters: - intmat (2D-array) – Matrix with non-negative integers.
- maxint (int) – Maximum allowed integer in intmat. Determines the length of the unit vectors. Must be greater than or equal to the actual maximum value in intmat.
Returns: binmat – If intmat has shape (m, n), then the shape of binmat is (maxint * m, n).
Return type: 2D-array
See also
Examples
>>> from strainpycon.utils import intmat2binmat >>> mat = np.array([[0, 1, 2], [2, 1, 0]]) >>> mat array([[0, 1, 2], [2, 1, 0]]) >>> intmat2binmat(mat, 2) array([[0, 1, 0], [0, 0, 1], [0, 1, 0], [1, 0, 0]])